CS131, Homewrok0, Basics

发表于 更新于 分类于
CS131 Computer Vision： Foundations and Applications，Homework0：Basics。
重点在如何用python和numpy操作图像，顺带实现一些基本的线性代数计算。

Homework 0

在这个作业中，我们将使用python进行基本的线性代数和图像处理，这些是这门课程的必备技能。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
#Imports the print function from newer versions of python
from __future__ import print_function

#Setup

# The Random module for implements pseudo-random number generators
import random 

# Numpy is the main package for scientific computing with Python. 
# This will be one of our most used libraries in this class
import numpy as np


#Imports all the methods in each of the files: linalg.py and imageManip.py
from linalg import *
from imageManip import *


#Matplotlib is a useful plotting library for python 
import matplotlib.pyplot as plt
# This code is to make matplotlib figures appear inline in the
# notebook rather than in a new window.
%matplotlib inline
plt.rcParams['figure.figsize'] = (10.0, 8.0) # set default size of plots
plt.rcParams['image.interpolation'] = 'nearest'
plt.rcParams['image.cmap'] = 'gray'

# Some more magic so that the notebook will reload external python modules;
# see http://stackoverflow.com/questions/1907993/autoreload-of-modules-in-ipython
%load_ext autoreload
%autoreload 2
%reload_ext autoreload
The autoreload extension is already loaded. To reload it, use:
  %reload_ext autoreload

Question 1: Linear Algebra Review

Please implement all the required methods in linalg.py.

任务：实现 linalg.py 中的方法

Question 1.1 (5 points)

Define the following using numpy:

$$
M = \begin{bmatrix}
1 & 2 & 3 \\
4 & 5 & 6 \\
7 & 8 & 9 \\
10 & 11 & 12 \end{bmatrix}
$$

$$
a = \begin{bmatrix}
1 & 1 & 0
\end{bmatrix}
$$

$$
b = \begin{bmatrix}
-1 \\ 2 \\ 5
\end{bmatrix}
$$ 

1
2
3
4
5
6
7
8
### YOUR CODE HERE
M = np.array([[1,2,3],[4,5,6],[7,8,9],[10,11,12]])
a = np.array([1,1,0])
b = np.array([[-1],[2],[5]])
### END CODE HERE
print("M = \n", M)
print("a = ", a)
print("b = ", b)
M = 
 [[ 1  2  3]
 [ 4  5  6]
 [ 7  8  9]
 [10 11 12]]
a =  [1 1 0]
b =  [[-1]
 [ 2]
 [ 5]]

Question 1.2 (5 points)

Implement the dot_product method in linalg.py and check that it returns the correct answer for $a^Tb$.

点乘/内积

numpy函数：np.dot

1
2
aDotB = dot_product(a, b)
print (aDotB)
[1]

Question 1.3 (5 points)

Implement the matrix_mult method in linalg.py and use it to compute $(a^T b)Ma$

矩阵乘法

numpy函数：np.matmul(

1
2
ans = matrix_mult(M, a, b)
print (ans)
[ 3  9 15 21]

Question 4 (10 points)

Implement the get_singular_values method. In this method, perform singular value decomposition on the input matrix and return the largest n singular values (n specified in the method calls below).

使用SVD方法进行奇异值分解

numpy函数：np.linalg.svd

1
2
print(get_singular_values(M, 1))
print(get_singular_values(M, 2))
[ 25.46240744]
[ 25.46240744   1.29066168]

Question 1.5 (10 points)

Implement the get_eigen_values_and_vectors method. In this method, perform eigen value decomposition on the following matrix and return the largest n eigen values and corresponding eigen vectors (n specified in the method calls below).

特征分解，计算特征值和特征向量

numpy函数：np.linalg.eig

$$
M = \begin{bmatrix}
1 & 2 & 3 \\
4 & 5 & 6 \\
7 & 8 & 9 \end{bmatrix}
$$

1
2
3
4
5
6
7
M = np.matrix([[1,2,3],[4,5,6],[7,8,9]])
val, vec = get_eigen_values_and_vectors(M[:,:3], 1)
print("Values = \n", val)
print("Vectors = \n", vec)
val, vec = get_eigen_values_and_vectors(M[:,:3], 2)
print("Values = \n", val)
print("Vectors = \n", vec)
Values = 
 [ 16.11684397]
Vectors = 
 [[-0.23197069 -0.78583024  0.40824829]]
Values = 
 [ 16.11684397  -1.11684397]
Vectors = 
 [[-0.23197069 -0.78583024  0.40824829]
 [-0.52532209 -0.08675134 -0.81649658]]

Part 2: Image Manipulation

1
2
image1_path = './image1.jpg'
image2_path = './image2.jpg'

Question 2.1 (5 points)

Implement the load method in imageManip.py and read the display method below. We will use these two methods through the rest of the notebook to visualize our work.

加载图像

skimage函数：io.imread

1
2
3
4
5
def display(img):
    # Show image
    plt.imshow(img)
    plt.axis('off')
    plt.show()
1
2
3
4
5
image1 = load(image1_path)
image2 = load(image2_path)

display(image1)
display(image2)

png

png

Question 2.2 (10 points)

Implement the change_value method by converting images according to $x_n = 0.5*x_p^2$ for every pixel, where $x_n$ is the new value and $x_p$ is the original value.

利用np.multiply函数直接对图像矩阵做乘法

1
2
new_image = change_value(image1)
display(new_image)

png

Question 2.3 (10 points)

Implement the convert_to_grey_scale method and convert the image into grey scale.

调用color.rgb2gray()

1
2
grey_image = convert_to_grey_scale(image1)
display(grey_image)

png

Question 2.4 (10 points)

Implement the rgb_decomposition, in which the input image is decomposed into the three channels: R, G and B and return the image excluding the specified channel.

RGB分解，在scikitimage中，R，G，B分别对应numpy的0,1,2三个通道。
除去RGB某个通道，即指定哪个通道则让该通道的值为零。

此处注意图像的深拷贝与浅拷贝，如直接对image1进行操作，每次都作用在image1上，三次操作之后，image1为（0,0,0）

1
2
3
4
5
6
7
without_red = rgb_decomposition(image1, 'R')
without_blue = rgb_decomposition(image1, 'B')
without_green = rgb_decomposition(image1, 'G')

display(without_red)
display(without_blue)
display(without_green)

png

png

png

Question 2.5 (10 points)

Implement the lab_decomposition, in which the input image is decomposed into the three channels: L, A and B and return the values for the specified channel.

LAB分解，在scikitimage中，L，A，B分别对应numpy的0,1,2三个通道

color.rgb2lab将图像进行RGB->LAB空间。

然后选取某通道

1
2
3
4
5
6
7
image_l = lab_decomposition(image1, 'L')
image_a = lab_decomposition(image1, 'A')
image_b = lab_decomposition(image1, 'B')

display(image_l)
display(image_a)
display(image_b)

png

png

png

Question 2.6 (10 points)

Implement the hsv_decomposition, in which the input image is decomposed into the three channels: H, S and V and return the values for the specified channel.

HSV分解，在scikitimage中，H,S,V分别对应numpy的0,1,2三个通道

调用color.rgb2hsv进行RGB->HSV转换

然后选取某通道

1
2
3
4
5
6
7
image_h = hsv_decomposition(image1, 'H')
image_s = hsv_decomposition(image1, 'S')
image_v = hsv_decomposition(image1, 'V')

display(image_h)
display(image_s)
display(image_v)

png

png

png

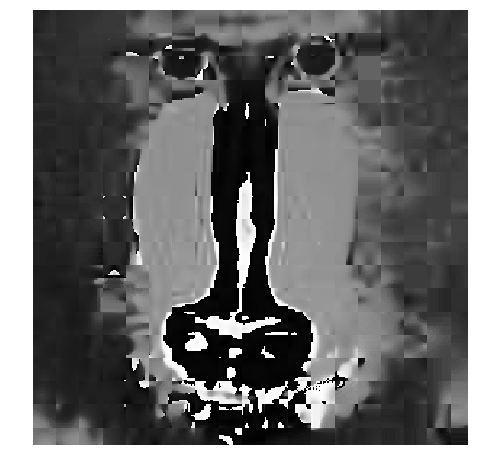
Question 2.7 (10 points)

In mix_images method, create a new image such that the left half of the image is the left half of image1 and the
right half of the image is the right half of image2. If the channels are specified, exclude the specified channel for the given image.

numpy函数np.concatenate进行矩阵的拼接。

1
2
image_mixed = mix_images(image1, image2, channel1='R', channel2='G')
display(image_mixed)

png

代码档案

官方Repo作业材料

个人Repo作业存档